Question

Pls help me answer this

Diagram 3 shows a composite solid, formed by joining a half m-cylinder with a right prism. ABKJ is the cross - section of the right prism. MK is the diameter of the half - cylinder Given BK 28 cm, AJ = 14 and AE = 20 cm, The volume of the composite solid is 17000 cm³
Using

`\pi = (22)/(7)`
calculate the value of h

​

Answer 1

Answer: 30 cm

Explanation:

The volume of the composite solid is 17000 cm³. To find h, we must first subtract the volume of the half cylinder from the composite volume.

From the figure, AE = MK, and so the radius of the half cylinder is 10cm. The volume of the half cylinder is thus
`(1)/(2)` the volume of a cylinder. The volume of a cylinder is πr²h. So a half cylinder is 1/2 πr²h. This gives us a volume of
`(1)/(2) ((22)/(7))(10 cm)^2(28 cm) = 4400 cm^3`.

Thus, the volume of the right prism is 17000cm³ - 4400cm³ = 12600cm³. Consider the cross-section ABKJ. If we multiply this by AE, we'll have the volume of the right prism.

The ABKJ is a trapezoid so it's area is
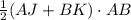`(1)/(2)(AJ + BK) \cdot AB`. Thus the volume of the right prism is
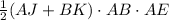`(1)/(2)(AJ + BK) \cdot AB \cdot AE`. This gives us
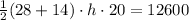`(1)/(2)(28 + 14) \cdot h \cdot 20 = 12600`, and thus h = 30 cm.