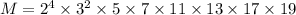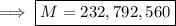Consider the prime factorization of 20!.
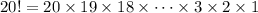
The LCM of 1, 2, ..., 20 must contain all the primes less than 20 in its factorization, so
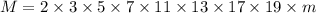
where
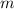 is some integer not divisible by any of these primes.
is some integer not divisible by any of these primes.
Compare the factorizations of the remaining divisors of 20!, and check off any whose factorizations are already contained in the product of primes above.
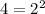 - missing a factor of 2
- missing a factor of 2
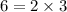 - ✓
- ✓
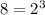 - missing a factor of 2²
- missing a factor of 2²
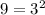 - missing a factor of 3
- missing a factor of 3
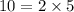 - ✓
- ✓
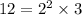 - missing a factor of 2
- missing a factor of 2
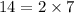 - ✓
- ✓
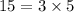 - ✓
- ✓
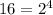 - missing a factor of 2³
- missing a factor of 2³
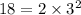 - missing a factor of 3
- missing a factor of 3
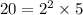 - missing a factor of 2
- missing a factor of 2
From the divisors marked "missing", we add the necessary missing factors to the factorization of
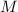 , so that
, so that
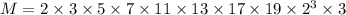
Then the LCM of 1, 2, 3, …, 20 is