Question

Question 6 The volumes of two similar solids are 729m3 and 125m3 The surface area of the larger solid is 324m2. What is the surface area of the smaller solid

Answer 1

100 m²

Explanation:

The scale factor for volume of similar figures is the cube of the scale factor for linear dimensions. The scale factor for area is the square of that linear dimension scale factor.

Scale factor

If the ratio of volumes is the cube of the scale factor, then the scale factor for the smaller figure in terms of the larger is ...

`k=\sqrt[3]{\frac{125\text{ m}^3}{729\text{ m}^3}}=\sqrt[3]{(5^3)/(9^3)}=(5)/(9)`

Smaller area

The area of the smaller figure is found from ...

`\frac{A}{324\text{ m}^2}=\left((5)/(9)\right)^2=(25)/(81)\\\\A=(324\text{ m}^2)\cdot(25)/(81)=\boxed{100\text{ m}^2}`

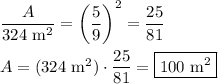
The surface area of the smaller solid is 100 square meters.

__

Additional comment

The least surface area for a given volume is that of a sphere. The larger volume given corresponds to a sphere with a radius of about 5.583 meters. Such a sphere will have an area of about 391.7 square meters. There is no known physical object with a volume of 729 m³ that can have a surface area as little as 324 m².