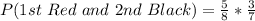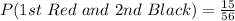Answer:
For probabilities with replacement
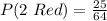

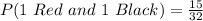
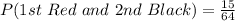
For probabilities without replacement
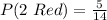
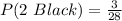
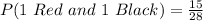
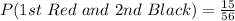
Explanation:
Given
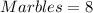
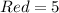
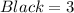
For probabilities with replacement
(a) P(2 Red)
This is calculated as:
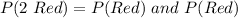

So, we have:
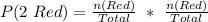
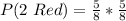
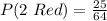
(b) P(2 Black)
This is calculated as:
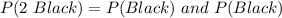
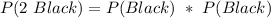
So, we have:
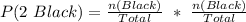
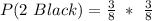

(c) P(1 Red and 1 Black)
This is calculated as:
![P(1\ Red\ and\ 1\ Black) = [P(Red)\ and\ P(Black)]\ or\ [P(Black)\ and\ P(Red)]](https://img.qammunity.org/2022/formulas/mathematics/college/1mki1xn8ba5m73qj9gvv7za2sip7fgir92.png)
![P(1\ Red\ and\ 1\ Black) = [P(Red)\ *\ P(Black)]\ +\ [P(Black)\ *\ P(Red)]](https://img.qammunity.org/2022/formulas/mathematics/college/455lldqn0wuoeno80pavvmzus1icb34722.png)
![P(1\ Red\ and\ 1\ Black) = 2[P(Red)\ *\ P(Black)]](https://img.qammunity.org/2022/formulas/mathematics/college/63irukx1mvl54foyjmqm0lo1p0pjiqm0h3.png)
So, we have:
![P(1\ Red\ and\ 1\ Black) = 2*[(5)/(8) *(3)/(8)]](https://img.qammunity.org/2022/formulas/mathematics/college/6gzv3av2w7mz62s1navitkt01ca744zxuf.png)
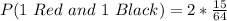
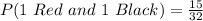
(d) P(1st Red and 2nd Black)
This is calculated as:
![P(1st\ Red\ and\ 2nd\ Black) = [P(Red)\ and\ P(Black)]](https://img.qammunity.org/2022/formulas/mathematics/college/jrd3t7cayi0l47gwy90m8vrb8837cqogrd.png)
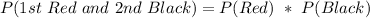
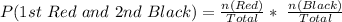
So, we have:
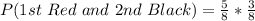
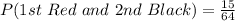
For probabilities without replacement
(a) P(2 Red)
This is calculated as:
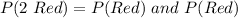

So, we have:
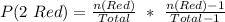
We subtracted 1 because the number of red balls (and the total) decreased by 1 after the first red ball is picked.
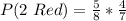
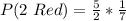
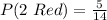
(b) P(2 Black)
This is calculated as:
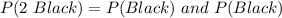
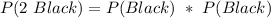
So, we have:

We subtracted 1 because the number of black balls (and the total) decreased by 1 after the first black ball is picked.
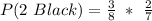
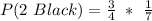
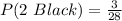
(c) P(1 Red and 1 Black)
This is calculated as:
![P(1\ Red\ and\ 1\ Black) = [P(Red)\ and\ P(Black)]\ or\ [P(Black)\ and\ P(Red)]](https://img.qammunity.org/2022/formulas/mathematics/college/1mki1xn8ba5m73qj9gvv7za2sip7fgir92.png)
![P(1\ Red\ and\ 1\ Black) = [P(Red)\ *\ P(Black)]\ +\ [P(Black)\ *\ P(Red)]](https://img.qammunity.org/2022/formulas/mathematics/college/455lldqn0wuoeno80pavvmzus1icb34722.png)
![P(1\ Red\ and\ 1\ Black) = [(n(Red))/(Total)\ *\ (n(Black))/(Total-1)]\ +\ [(n(Black))/(Total)\ *\ (n(Red))/(Total-1)]](https://img.qammunity.org/2022/formulas/mathematics/college/m4it0xssntpmc6n62xob4cus6uz8clv0xt.png)
So, we have:
![P(1\ Red\ and\ 1\ Black) = [(5)/(8) *(3)/(7)] + [(3)/(8) *(5)/(7)]](https://img.qammunity.org/2022/formulas/mathematics/college/kgz69d9embrg723kcsutuxildzbpldk57t.png)
![P(1\ Red\ and\ 1\ Black) = [(15)/(56) ] + [(15)/(56)]](https://img.qammunity.org/2022/formulas/mathematics/college/5hx2n33nkr94c2bwjde360s1qtbz21h6mb.png)
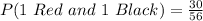
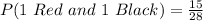
(d) P(1st Red and 2nd Black)
This is calculated as:
![P(1st\ Red\ and\ 2nd\ Black) = [P(Red)\ and\ P(Black)]](https://img.qammunity.org/2022/formulas/mathematics/college/jrd3t7cayi0l47gwy90m8vrb8837cqogrd.png)
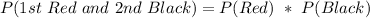
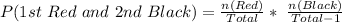
So, we have: