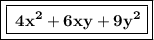
- 8x cube minus 27y cube divided by 2x minus 3y.
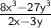
Factor the expressions that are not already factored.
How to factorise :-
Rewrite
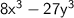 as
as
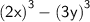 . The difference of cubes can be factored using the algebraic rule:
. The difference of cubes can be factored using the algebraic rule:
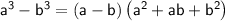 .
.
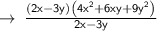
Cancel out 2x-3y in both the numerator and denominator.