Question

Round your answer to the nearest whole number

Answer 1

`\huge \red \dag \underline {\rm {{{\color{orange}{Given ...}}}}} \red \dag`

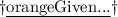
• Diagonal of TV screen = 42 inches
• Base of TV screen = 38 inches

`\huge \red \dag \underline {\rm {{{\color{orange}{To \: Find ...}}}}} \red \dag`

• Height of TV

`\huge \red \dag \underline {\rm {{{\color{orange}{Solution ...}}}}} \red \dag`

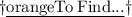
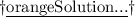
Answer according to the figure in attachment

In this situation we use Pythagoras theorem.

• Pythagoras theorem states that “In a right-angled triangle, the square of the hypotenuse side is equal to the sum of squares of the other two sides“.

According to Pythagoras theorem

`\Large❏ \: \Large\begin{gathered} {\underline{\boxed{ \tt {\blue{BD² = BC² + DC²}}}}}\end{gathered}`

• BD = 42 inches
• BC = 38 inches
• DC = ?

We need to find the DC.

Substituting the values in Pythagoras theorem

`\large\purple\implies \tt \large \:BD² = BC² + DC²`

`\large\purple\implies \tt \large \: {42}^(2) \: = \: {38}^(2) \: + \: DC²`

`\large\purple\implies \tt \large \:1764 \: = \: 1444 \: + \: DC²`

`\large\purple\implies \tt \large \:1764 \: - \: 1444 \: = \: DC²`

`\large\purple\implies \tt \large \:320 \: = \: DC²`

`\large\purple\implies \tt \large \: √(320) \: = \: DC`

`\large\purple\implies \tt \large \:17.88 \: = \: DC`

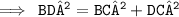
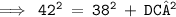
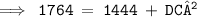
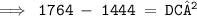
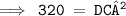
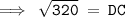
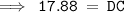
Hence , the height of TV is 17.88 inches

Answer 2

Explanation:

Comment

• Use a^2 + b^2 = c^2
• b = 38
• c = 42
• a = ?

Solution

a^2 + b^2 = c^2

a^2 + 38^2 = 42^2

a^2 + 1444 =1764 Subtract 1444 from both sides

a^2 + 1444 - 1444 = 1764 - 1444 Combine

a^2 = 320 Take the square root of both sides

√a^2 = √320

a = 17.89

Answer

The height of the TV screen is 17.89 inches