Question

Suppose you invest in an annuity that pays 6% interest, compounded annually. You contribute $4,500 each year for 10

years, what is the value of the annuity at the end of 10 years? Enter your answer rounded to the nearest hundred dollars.
Omit the dollar sign and comma ($42,570.21 should be entered as 42600.)

Answer 1

The future value of an annuity that has annual payments of $4,500 at a 6% annual interest rate, compounded annually for 10 years, can be calculated using the future value of an annuity formula. After performing the required computations and rounding to the nearest hundred dollars, you'll get the final amount ready for input.

Step-by-step explanation:

To calculate the value of an annuity that pays 6% interest, compounded annually, with annual contributions of $4,500 for 10 years, we use the future value of an annuity formula:

FV = P ×
`{[ (1 + r)^(n - 1 ] / r)`

Where:
FV is the future value of the annuity
P is the annual payment ($4,500)
r is the annual interest rate (0.06 for 6%)
n is the total number of payments (10)

Plugging in the values:

FV = $4,500 × {[
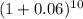`(1 + 0.06)^{10` - 1 ] / 0.06}

Calculate the bracketed term first, (1 + 0.06)^10, then subtract 1, and finally divide by 0.06. Multiply this result by $4,500 to get the future value.

Once calculated, the answer should be rounded to the nearest hundred dollars as specified. For example, if you get an answer like $42,570.21, you would round this to 42600 (as requested, without the dollar sign or comma).

Remember, the power of compounding greatly affects the growth of investments. Over time, the amount you receive from interest will grow as it compounds, leading to a larger sum at the end of the annuity term.