Question

3.16 SAT scores: SAT scores (out of 2400) are distributed normally with a mean of 1490 and a standard deviation of 295. Suppose a school council awards a certificate of excellence to all students who score at least 1900 on the SAT, and suppose we pick one of the recognized students at random. What is the probability this student's score will be at least 2100

Answer 1

To find the probability that a student awarded a certificate of excellence for scoring at least 1900 on the SAT scores at least 2100, calculate the z-score for 2100 and refer to a normal distribution table or calculator to determine the corresponding probability in the upper tail of the distribution.

Step-by-step explanation:

Calculating the Probability of an SAT Score

To find the probability that a randomly selected student who received a certificate of excellence scores at least 2100 on the SAT, we must first understand that the SAT scores are normally distributed with a mean (µ) of 1490 and a standard deviation (σ) of 295. Since the certificate of excellence is awarded for scores at least 1900, we are only considering the upper tail of the distribution.

To calculate this probability, we need to find the z-score for 2100.

Z = (X - µ) / σ, where X is the SAT score of interest.

Z = (2100 - 1490) / 295 ≈ 2.07

Using a z-score table or a normal distribution calculator, we can find the probability associated with a z-score of 2.07. However, since we need the probability of scoring at least 2100, we are interested in the area to the right of this z-score, which can be found by subtracting the table value from 1.

(This portion would be completed using a z-score table or calculator)

The probability of a recognized student scoring at least 2100 on the SAT is therefore the complement of the z-score table value for 2.07.

Answer 2

0.2333 = 23.33% probability this student's score will be at least 2100.

Step-by-step explanation:

To solve this question, we need to understand the normal probability distribution, and conditional probability.

Normal Probability Distribution:

Problems of normal distributions can be solved using the z-score formula.

In a set with mean
`\mu` and standard deviation
`\sigma`, the zscore of a measure X is given by:

`Z = (X - \mu)/(\sigma)`

The Z-score measures how many standard deviations the measure is from the mean. After finding the Z-score, we look at the z-score table and find the p-value associated with this z-score. This p-value is the probability that the value of the measure is smaller than X, that is, the percentile of X. Subtracting 1 by the pvalue, we get the probability that the value of the measure is greater than X.

Conditional Probability

We use the conditional probability formula to solve this question. It is

`P(B|A) = (P(A \cap B))/(P(A))`

In which

P(B|A) is the probability of event B happening, given that A happened.

`P(A \cap B)` is the probability of both A and B happening.

P(A) is the probability of A happening.

SAT scores (out of 2400) are distributed normally with a mean of 1490 and a standard deviation of 295.

This means that
`\mu = 1490, \sigma = 295`

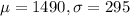
In this question:

Event A: Student was recognized.

Event B: Student scored at least 2100.

Probability of a student being recognized:

Probability of scoring at least 1900, which is 1 subtracted by the pvalue of Z when X = 1900. So

`Z = (X - \mu)/(\sigma)`

`Z = (1900 - 1490)/(295)`

`Z = 1.39`

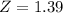
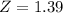`Z = 1.39` has a pvalue of 0.9177

1 - 0.9177 = 0.0823

This means that
`P(A) = 0.0823`

Probability of a student being recognized and scoring at least 2100:

Intersection between at least 1900 and at least 2100 is at least 2100, so this is 1 subtracted by the pvalue of Z when X = 2100.

`Z = (X - \mu)/(\sigma)`

`Z = (2100 - 1490)/(295)`

`Z = 2.07`

`Z = 2.07` has a pvalue of 0.9808

This means that
`P(A \cap B) = 1 - 0.9808 = 0.0192`

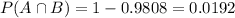
What is the probability this student's score will be at least 2100?

`P(B|A) = (P(A \cap B))/(P(A)) = (0.0192)/(0.0823) = 0.2333`

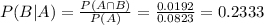
0.2333 = 23.33% probability this student's score will be at least 2100.