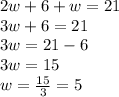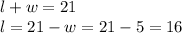Answer:
The length of the garden is 16 ft while the width of the garden is 5 ft.
Step-by-step explanation:
a)we want to start with defining the variables.
Let the length of the garden be w.
b) here, we want to create equation
From the question, the length is 6 feet more than twice the width of one garden
Mathematically, we have this as;
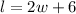
Furthermore, the perimeter is 42 feet
The formula of the perimeter is;

Dividing both sides by 2
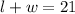
c)Now, we want to solve both equations simultaneously
We can substitute the first equation into the second;