Question

Using traditional methods, it takes 95 hours to receive a basic flying license. A new license training method using Computer Aided Instruction (CAI) has been proposed. A researcher used the technique with 260 students and observed that they had a mean of 94 hours. Assume the standard deviation is known to be 6. A level of significance of 0.01 will be used to determine if the technique performs differently than the traditional method. Is there sufficient evidence to support the claim that the technique performs differently than the traditional method

Answer 1

There is not sufficient evidence to support the claim that the technique performs differently than the traditional method.

Explanation:

The null hypothesis is:

`H_(0) = 95`

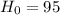
The alternate hypotesis is:

`H_(1) \\eq 95`

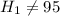
The test statistic is:

`z = (X - \mu)/((\sigma)/(√(n)))`

In which X is the sample mean,
`\mu` is the value tested at the null hypothesis,
`\sigma` is the standard deviation and n is the size of the sample.

A researcher used the technique with 260 students and observed that they had a mean of 94 hours. Assume the standard deviation is known to be 6.

This means, respectively, that
`n = 260, X = 94, \sigma = 6`

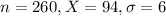
The test-statistic is:

`z = (X - \mu)/((\sigma)/(√(n)))`

`z = (94 - 95)/((6)/(√(260)))`

`z = -2.69`

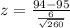
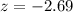
The pvalue is:

2(P(Z < -2.69))

P(Z < -2.69) is the pvalue of Z when X = -2.69, which looking at the z-table, is 0.0036

2*(0.0036) = 0.0072

0.0072 < 0.01, which means that the null hypothesis is accepted, that is, there is not sufficient evidence to support the claim that the technique performs differently than the traditional method.