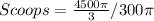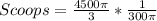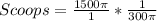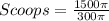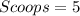Answer:
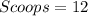 --- cup 1
--- cup 1
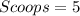 --- cup 2
--- cup 2
Explanation:
Given
Hemisphere
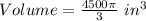
Cup 1
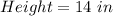
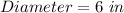
Cup 2
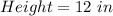
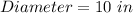
Required: How many scoop of each?
For cup 1
Calculate the volume
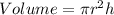
Where
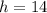
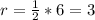
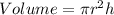
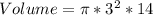
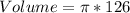
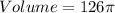
Divide the volume of the hemisphere by the calculated volume of cup 1
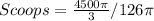
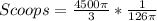
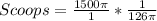
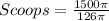
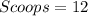 --- approximated
--- approximated
For cup 2
Calculate the volume
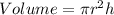
Where
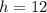
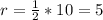
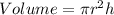
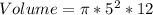
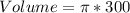
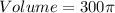
Divide the volume of the hemisphere by the calculated volume of cup 2