Question

Three vertices of a parallelogram are shown in the figure below.

Give the coordinates of the fourth vertex.
(-3,9)
(0,-3) (6,-6)

Answer 1

Given:

The three vertices of the parallelogram are (-3,9), (0,-3), (6,-6).

To find:

The fourth vertex of the parallelogram.

Solution:

Consider the three vertices of the parallelogram are A(-3,9), B(0,-3), C(6,-6).

Let D(a,b) be the fourth vertex.

Midpoint formula:

`Midpoint=\left((x_1+x_2)/(2),(y_1+y_2)/(2)\right)`

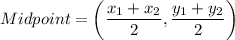
We know that the diagonals of a parallelogram bisect each other. So, the midpoints of both diagonals are same.

Midpoint of AC = Midpoint BD

`\left((-3+6)/(2),(9+(-6))/(2)\right)=\left((0+a)/(2),(-3+b)/(2)\right)`

`\left((3)/(2),(3)/(2)\right)=\left((a)/(2),(-3+b)/(2)\right)`

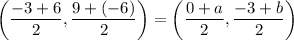
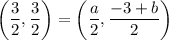
On comparing both sides, we get

`(3)/(2)=(a)/(2)`

`3=a`

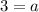
And,

`(3)/(2)=(-3+b)/(2)`

`3=-3+b`

`3+3=b`

`6=b`

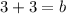
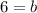
Therefore, the fourth vertex of the parallelogram is (3,6).