Question

John is planning to build a shelf in the shape of a right triangle. He recorded the possible side lengths of the shelf in the table below. Will the side lengths recorded form the shelf?

9, 40, 41 yes or no
11, 60, 62 yes or no
48, 55, 73 yes or no

Answer 1

The first two sets satisfy the Pythagorean Theorem
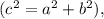`(\(c^2 = a^2 + b^2\)),` confirming they form right triangles. However, the third set does not meet this condition, indicating it does not represent a right-angled triangle.

Step-by-step explanation:

The first set of side lengths, 9, 40, 41, satisfies the Pythagorean Theorem, where
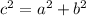`\(c^2 = a^2 + b^2\)` . In this case,
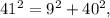`\(41^2 = 9^2 + 40^2\),` resulting in
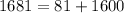`\(1681 = 81 + 1600\)` . The equality holds, affirming that the set forms a right-angled triangle. Similarly, the second set, 11, 60, 62, also conforms to the Pythagorean Theorem:
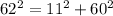`\(62^2 = 11^2 + 60^2\)` , leading to
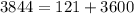`\(3844 = 121 + 3600\)` . This equality validates that the second set represents a right triangle.

Similarly, for the set 11, 60, 62, the Pythagorean Theorem holds true
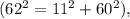`(\(62^2 = 11^2 + 60^2\)),` providing evidence that this set fulfills the criteria for a right-angled triangle. Consequently, a shelf with sides of 11, 60, and 62 units would also be suitable for construction.

Conversely, the third set, 48, 55, 73, does not meet the Pythagorean condition:
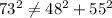`\(73^2 \\eq 48^2 + 55^2\)` . The resulting calculation,
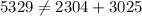`\(5329 \\eq 2304 + 3025\)` , demonstrates that the third set does not form a right-angled triangle. Therefore, the shelf with side lengths 48, 55, and 73 is not feasible. In conclusion, the first two sets of side lengths are suitable for constructing a shelf in the shape of a right triangle, while the third set does not meet the necessary geometric conditions.

Answer 2

A^2 + b^2 = c2

Step-by-step explanation:

Where the longest side length is the hypotenuse, or c.

9^2 + 40^2 = 41^2

81 + 1600 = 1681.this is a true statement, therefore "yes"

121 + 3600 = 3844 this is not a true statement, "no"

2304 + 3025 = 5329 "yes"