Question

Determine whether the following equation represents a direct variation If it does, find the constant of variation

2x + 3y = 0

Answer 1

Given:

The equation is

`2x+3y=0`

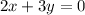
To find:

Whether the equation represents a direct variation. If it does, find the constant of variation.

Solution:

The general equation of direct variation is

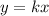`y=kx` ...(i)

Where, k is the constant of variation.

The equation of direct variation is always true for (0,0).

The given equation is

`2x+3y=0`

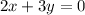
It can be written as

`3y=-2x`

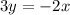
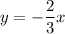`y=-(2)/(3)x` ...(ii)

For x=0,

`y=-(2)/(3)(0)`

`y=0`

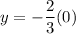
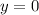
The given equation is true for (0,0). So, it represents a direct variation.

On comparing (i) and (ii), we get

`k=-(2)/(3)`

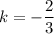
Therefore, the constant of variation is
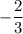`-(2)/(3)`.