Answer:
The distance is 2077.77m
Explanation:
Given
Represent speed with s and time with t
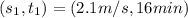 ---- Left
---- Left
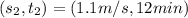 --- South
--- South
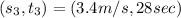 ---- Right
---- Right
Required
How far are you from your car?
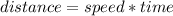
To solve this question, I will use the attached image to illustrate the movement.
First, we calculate distance AB
Using:
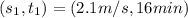 ---- Left
---- Left
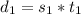
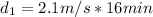
Convert min to secs

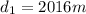

Next, we calculate the distance BC
Using:
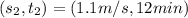 --- South
--- South
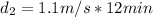
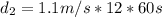

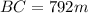
Next, we calculate distance CD
Using:
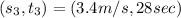 ---- Right
---- Right
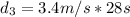
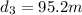
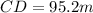
The distance between you and the car is represented as AD.
Considering triangle AOD, we have:

Where:
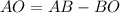
and
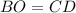
So:
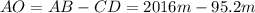


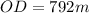
The equation becomes:

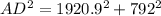
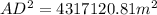


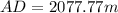 --- approximated
--- approximated