Question

You are traveling down a country road at a rate of 95 feet/sec when you see a large cow 300 feet in front of you and directly in your lane. The cow is fearless, and staring you down. (Or perhaps she does not understand the gravity of the situation.) Regardless, if you simply hit your brakes, after t seconds, the car will be j(t) = 95t - 9t^2 feet from the point where the brakes were first applied.

1) Must you steer to avoid the cow, or can you rely solely on your brakes? Explain.
2) Graph J(t), j'(t), and j"(t) and Interpret their meanings in context.
3) Is there a time t after which the graphs in part (ii) probably do not accurately model the path of the car?
4) Write a piece-wise function using j(t) that would more accurately model the path of the car on the interval [0, 10], assuming the car did not move after it stopped. Sketch this graph and its derivative.

Answer 1

1) You can rely solely on your brakes because when doing so the car will just travel 250ft from the point you hit your brakes till the point the car stopped completely, leaving you 50ft away from the cow.

2) See attached picture.

j(t) represents the distance from the point you hit the brake t seconds after you hit it in feet

j'(t) represents the velocity of the car t seconds after the brakes have been hit in ft/s.

j"(t) represents the acceleration of the car t seconds after the brakes have been hit in
`ft/s^(2)`

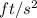
3) yes, any time after t=5.28 will not accurately model the path of the car since at that exact time the car will reach a velocity of 0ft/s and unless another force is applied to the car, then the car will not move after that time.

4)
`j(t)=\left \{ {{95t-9t^(2); 0\le t<5.28s} \atop {250.69; 5.28s\leq t \leq 10s}} \right.`

`j'(t)=\left \{ {{95-18t; 0\leq t<5.28s} \atop {0 ; 5.28s\leq t \leq 10s}} \right.`

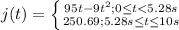
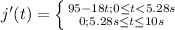
(see attached picture for graph)

Explanation:

1) In this part of the problem we need to find the time when the speed of the car is 0. Gets to a complete stop. For this we will need to take the derivative of the position function so we get:

`j(t)=95t-9t^2`

`j'(t)=95-18t`

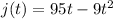
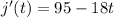
and we set the first derivative equal to zero so we get:

95-18t=0

and solve for t

-18t=-95

`t=(95)/(18)`

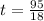
t=5.28s

so now we calculate the position of the car after 5.28 seconds, so we get:

`j(5.28)=95(5.28)-9(5.28)^(2)`

`j(5.28)=250.69ft`

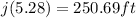
so we have that the car will stop 250.69ft after he hit the brakes, so there will be about 50ft between the car and the cow when the car stops completely, so he can rely just on the breaks.

2) For answer 2 I take the second derivative of the function so I get:

`j(t)=95t-9t^(2)`

`j'(t)=95-18t`

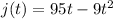
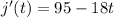
j"(t)=-18

and then we graph them. (See attached picture)

j(t) represents the distance from the point you hit the brake t seconds after you hit it in feet

j'(t) represents the velocity of the car t seconds after the brakes have been hit in ft/s.

j"(t) represents the acceleration of the car t seconds after the brakes have been hit in
`ft/s^(2)`

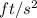
3) yes, any time after t=5.28 will not accurately model the path of the car since at that exact time the car will reach a velocity of 0ft/s and unless another force is applied to the car, then the car will not move after that time.

4)
`j(t)=\left \{ {{95t-9t^(2); 0\le t<5.28s} \atop {250.69; 5.28s\leq t \leq 10s}} \right.`

`j'(t)=\left \{ {{95-18t; 0\leq t<5.28s} \atop {0 ; 5.28s\leq t \leq 10s}} \right.`

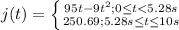
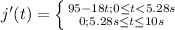
(see attached picture for graph)