Answer:
Following are the solution to these choices:
Explanation:
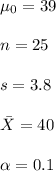
The test assumption is:
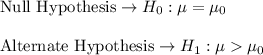
It is a checked right-tail, since the alternative hypothesis is produced to classify the argument when the data difference is greater than 0.
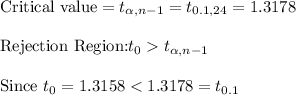
The null hypothesis should be rejected:
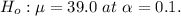
They have little enough proof that perhaps the average number of calls per person per week amounts to even more than 39.