you did not give the value for price. but here is the complete question
Joe has just moved to a smallJoe has just moved to a small town with only one golf course, the Northlands Golf Club. His inverse demand function is
p = 120 - 2 q,
where q is the number of rounds of golf that he plays per year. The manager of the Northlands Club negotiated separately with each person who joins the club and can therefore charge individual prices. This manager has a good idea of what Joe's demand curve is and offers Joe a special deal, where Joe pays an annual membership fee and can play as many rounds as he wants at $20, which is the marginal cost his round imposes on the Club. What membership fee would maximize profit for the Club? The manager could have charged Joe a single price per round. How much extra profit does the Club earn by using two-part pricing?
Answer:
membership fee = $2500
extra profit using 2 part pricing = $1250
Step-by-step explanation:
p = 120 - 2q
and price, p = 20 dollars = mc
20 = 120 - 2q
20-120 = -2q
-100 = -2q
q = 50
this is the quantity
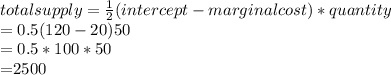
So the maximum membership fee is $2500
TR = PQ
= (120-2Q)Q
= 120-2Q²
we differentiate the above with respect to Q
MR = 120 - 4Q
MC = MR
20 = 120-4Q
20-120 = -4Q
-100 = -4Q
Q = 25
Remember
p = 120 - 2q
= 120 - 2x25
= 120-50
= 70
if single price is charged
(p-MC) x Q
= (70 - 20)x25
= 50 x 25
= $1250
by 2 par pricing, increase in profit would be
= $2500 - $1250
= $1250
thank you!