Question

Linda loves buying shoes and going out to dance. Her utility function for pairs of​ shoes, S, and the number of times she goes dancing per​ month, T,​ is: ​U(S, T)​ = 2ST with marginal​ utilities: MUS​ = 2T and MUT​ = 2S. It costs Linda ​$ to buy a new pair of shoes or to spend an evening out dancing. Assume that she has ​$ to spend on shoes and dancing. ​

1.) Use the line drawing tool to draw​ Linda's budget line. Label this line​ 'Budget'. ​
2.) Use the point drawing tool to locate​ Linda's optimal consumption bundle. Label this point​ 'R'. Carefully follow the instructions​ above, and only draw the required objects.

Answer 1

See Explanation

Step-by-step explanation:

Given

`U(S,T) = 2ST`

`M_U_S =2T`

`M_U_T=2S`

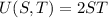
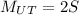
The following details are omitted from the question

`P_S= \$50` --- Price of the Shoes

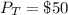`P_T = \$50` --- Spent on dancing

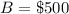`B = \$500` --- Budget on shoe and dancing

Solving (a): Her budget line

First, we determine her budget equation (B).

This is calculated by:

`B = P_S * S + P_T *T`

This gives:

`500 = 50 * S + 50 * T`

`500 = 50 S + 50 T`

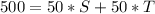
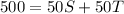
Divide through by 50

`10 =S + T`

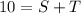
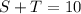`S + T = 10` --- The budget equation

See attachment for the budget line equation

Solving (a): Optimal Consumption Bundle Point

First, we determine the marginal rate of substitution (MRS) using:

`MRS = (MU_s)/(MU_t) = 1`

`MRS = (2S)/(2T) =1`

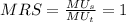
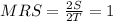
This implies that:

`(2S)/(2T) = 1`

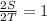
Cross Multiply

`2S = 2T * 1`

`2S = 2T`

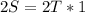
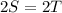
Divide by 2

`S = T`

Substitute T for S in the budget equation

`T + T= 10`

`2T = 10`

`T=5`

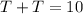
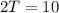
Recall that:

`S = T`

`S = 5`

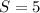
So, the point if optimal consumption bundle is (5,5)

See attachment for point R