Question

An 80-percent-efficient pump with a power input of 20 hp is pumping water from a lake to a nearby pool at a speed of 10 ft/s through a pipe of constant diameter 5.2 inches. The free surface of the pool is 80 ft above that of the lake. Determine the mass flow rate through the pipe and the mechanical power used to overcome frictional effects in piping. Take density of water to be 62.4 lbm/ft3

Answer 1

Part A

The mass plow rate, is approximately 97.0 lbm/s

Part B

The power used to overcome friction, is approximately 1.9 hp

Step-by-step explanation:

The efficiency of the pump, η = 80%

The power input to the pump, P = 20 hp

The speed of the water through the pipe, v = 10 ft./s

The diameter of the pipe, d = 5.2 inches = 13/30 ft.

The free surface of the pool above the lake, h = 80 ft.

The density of the water, ρ = 62.4 lbm/ft.³

Part A

The mass plow rate,
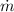`\dot m` = Q × ρ

Where;

ρ = 62.4 lbm/ft³

Q = A × v

A = The cross-sectional area of the pipe

∴ Q = π·d²/4 × v = π × ((13/30 ft.)²)/4 × 10 ft.s ≈ 1.4748 ft.³/s

∴ The mass plow rate,
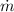`\dot m` ≈ 1.4748 ft.³/s × 62.4 lbm/ft.³ = 97.02752 lbm/s

The mass plow rate,
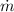`\dot m` ≈ 97.0 lbm/s

Part B

The power to pump the water at the given rate,
`P_w` =
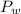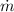`\dot m`·g·h

∴
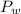`P_w` = 97.02752 lbm/s × 32.1740 ft./s² × 80 ft. ≈ 14.1130725 Hp

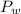`P_w` ≈ 14.1130725 Hp

The power output of the pump,
`P_(out)` = 0.8 × 20 hp = 16 hp

Therefore, the power used to overcome friction,
`P_f` =
`P_(out)` -
`P_w`

∴
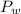
`P_f` ≈ 16 hp - 14.1130725 Hp ≈ 1.8869275 hp

The power used to overcome friction,
`P_f` ≈ 1.9 hp