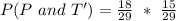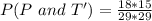Questions:
a. The jet ski is for two persons and has turbo packs.
b. The jet ski is not for two persons but has turbo packs.
Answer:
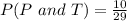

Explanation:
Given
 --- Total
--- Total
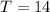 --- Two person skis
--- Two person skis
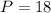 --- Turbo packs skis
--- Turbo packs skis
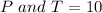 --- Two person ski and Turbo packs
--- Two person ski and Turbo packs
Solving (a):
This is represented as:
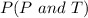
This is calculated as:
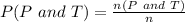
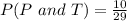
Solving (a):
This is represented as:
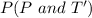
This is calculated as:

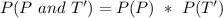
Using the complement rule, we have:
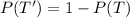
The equation becomes:
![P(P\ and\ T') = P(P)\ *\ [1 - P(T)]](https://img.qammunity.org/2022/formulas/mathematics/college/otfmrsn3g9db0d0sna8oqeiud8swi2yshb.png)
![P(P\ and\ T') = (n(P))/(n)\ *\ [1 - (n(T))/(n)]](https://img.qammunity.org/2022/formulas/mathematics/college/ms79hz0gba9ee1noq0m3ml8dovfhyifi8w.png)
![P(P\ and\ T') = (18)/(29)\ *\ [1 - (14)/(29)]](https://img.qammunity.org/2022/formulas/mathematics/college/bo75ueajsll1ghfoh2b2wy95e0rn3zbiri.png)