Question

There are 92 students in a chemistry class. The instructor must choose two students at random. Students in a Chemistry Class Academic Year Chemistry majors non-Chemistry majors Freshmen 15 15 Sophomores 13 9 Juniors 2 10 Seniors 12 16 What is the probability that a sophomore non-Chemistry major and then a junior non-Chemistry major are chosen at random

Answer 1

0.0108 = 1.08% probability that a sophomore non-Chemistry major and then a junior non-Chemistry major are chosen at random.

Explanation:

A probability is the number of desired outcomes divided by the number of total outcomes.

Probability that a sophomore non-Chemistry major

Out of 92 students, 9 are non-chemistry major sophomores. So

`P(A) = (9)/(92)`

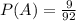
Then a junior non-Chemistry major are chosen at random.

Now, there are 91 students(1 has been chosen), of which 10 are non-chemistry major juniors. So

`P(B) = (10)/(91)`

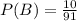
What is the probability that a sophomore non-Chemistry major and then a junior non-Chemistry major are chosen at random

`P = P(A)*P(B) = (9)/(92)*(10)/(91) = (9*10)/(92*91) = 0.0108`

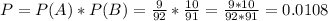
0.0108 = 1.08% probability that a sophomore non-Chemistry major and then a junior non-Chemistry major are chosen at random.