Question

A kite 40 ft above the ground moves horizontally at a constant speed of 10 ft/s, with a child, holding the ball of kite string, standing motionless on the ground. Assume the kite is flying away from the child. At what rate is the child releasing the string when (a) 50 ft of the string is out

Answer 1

v = 27.28 m /s, θ = 63.9º

Step-by-step explanation:

For this exercise we can approximate the movement to a projectile launch, let's analyze the situation.

* We must find the horizontal speed, for this we will find the descent time and the horizontal distance

* We look for the vertical speed

At the highest point the speed is horizontal

Let's find the time it takes for the kite to reach the ground

y = y₀ + v_{oy} t - ½ g t²

0 =y₀ + 0 -1/2 gt²

t =
`\sqrt{ (2y_o)/(g) }`

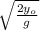
t = √(2 40/32)

t = 2.5 s

to find the horizontal velocity we must know the horizontal distance, let's use trigonometry

sin θ = y / l

θ = sin⁻¹1 y / l

θ = sin⁻¹ 40/50

θ = 53.1º

therefore the horizontal distance is

x = l cos 53.1

x = 50cos 53.1

x = 30 m

let's use the equation

x = v₀ₓ t

v₀ₓ = x / t

v₀ₓ = 30 / 2.5

v₀ₓ = 12 m / s

we look for the vertical component of the velocity

v_y = v_{oy} - g t

v_y = 0 - g t

v_y = - 9.8 2.5

v_y = -24.5 m / s

the negative sign indicates that the speed is directed downwards, because it is the arrival point, as they indicate that there is no friction, the exit speed is the same, worse with the opposite sign

We already have the two components of the velocity, let's use the Pythagorean theorem to find the modulus

v =
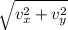
`√(v_x^2 + v_y^2)`

v =
`√(12^2 + 24.5^2)`

v = 27.28 m /s

we use trigonometry for the angle

tan θ = v_y / vₓ

θ = tan⁻¹ v_y / vₓ

θ = tan⁻¹ 24.5 / 12

θ = 63.9º