Question

Suppose you are an observer standing at a point along a three-lane roadway. All vehicles in lane 1 are traveling at 50 mi/hr with a constant 5-second time headway between them. All vehicles in lane 2 are traveling at 55 mi/hr with a constant 6-second time headway between them. All vehicles in lane 3 are traveling at 60 mi/hr with a constant 10-second time headway between them. You collected spot speed data for all vehicles as they crossed your observation point for 75 minutes. After 10 minutes, vehicles in lane 1 stopped arriving, and after 30 minutes, vehicles in lane 2 stopped arriving. What is the flow and density of the observed traffic stream

Answer 1

lane 3 Ф = 450 vehicles, ρ = 0.1 vehicle / s

lane 2 Ф_{average} = 300 vehicles, ρ _{average} = 6.66 10⁻² vehicles/s

lane 1 Ф_{average} = 300 vehicles, ρ_{average} = 2.66 10⁻² vehicle/s

Step-by-step explanation:

Before solving this exercise we must clarify the concepts the flow is defined as the occurrence of an event in a time interval, in this case the passage of a car through time

Flux Density is the flux between unit area or unit time

Let's start by calculating the calculation for lane 3

the flow.

Let's use a direct rule of proportions (rule three) if the number of vehicles per unit of time (t₀ = 10s), for the observation time how many vehicles passed in the observation time (t_total = 75 * 60 = 4500 s)

Ф = 4500 s (1 vehicle / 10 s)

Ф = 450 vehicles

The flux density is the flux per unit area, in this case the area is not indicated, so we can define the flux density as the flux per unit of time.

ρ = 450/4500

ρ = 0.1 vehicle / s

Lane 2

we look for the flow

we can have separates the interval into two parts

* for the first t₁1 = 30 * 60 = 1800 s

Ф₁ = 1800 s (1 vehicle / 6s)

Ф₁ = 300 vehicles during t₁

* for the rest of the time t₂ = 4500-1800 = 2700 s

Ф₂ = 0

the average density is the total number of vehicles between the total time

#_ {vehicle} = 300 +0

Ф_{average) = # _vehicle

Ф_{average} = 300 vehicles in all time

The density is

ρ 1 = fi1 / t1

ρ1 = 300/1800

ρ1 = 1.66 10-1 vehicles / s

the average density is

ρ_{average} =
`(\phi_1 + \phi_2)/( t_(total))`

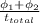
ρ _{average} = (300 +0) / 4500

ρ _{average} = 6.66 10⁻² vehicles / s

Lane 1

flow

* first time interval t₁ = 10 * 60 = 600 s

Ф₁ = 600 s (1 vehicle / 5s)

Ф₁ = 120 vehicles in interval t₁

* second interval t₂ = 4500-600 = 3900 s

Ф2 = 0

average flow

Ф = Ф1 + Ф2

Ф = 120 vehicles at all time

Density

* first interval

ρ₁ = 120/600

ρ₁ = 0.2 vehicles / s

* second interval

ρ₂ = 0

average density

ρ+{average} = 120/4500

ρ_{average} = 2.66 10⁻² vehicle/s