Question

A system consists of a copper tank whose mass is 13 kg, 4 kg of liquid water, and an electrical resistor of negligible mass. The system is insulated on its outer surface. Initially, the temperature of the copper is 27oC and the temperature of the water is 50oC. The electrical resistor transfers 120 kJ of energy to the system. Eventually the system comes to equilibrium. Determine the final equilibrium temperature (in oC).

Answer 1

T = 30.42°C

Step-by-step explanation:

According to the conservation of energy principle:

`Energy\ Given\ by\ Resistor = Heat\ Gain\ by\ Copper + Heat\ Gain\ by\ Water\\E = m_(c)C_(c)(T_(2c) - T_(1c)) + m_(w)C_(w)(T_(2w) - T_(1w))`

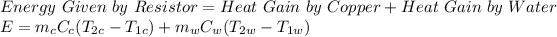
E = 120 KJ

mc = mass of copper = 13 kg

Cc = specific heat capacity of copper = 0.385 KJ/kg.°C

T2c = T2w = Final Equilibrium Temperature = T = ?

T1c = Initial Temperature of Copper = 27°C

T1w = Initial Temperature of Water = 50°C

mw = mass of water = 4 kg

Cw = specific heat capacity of water = 4.2 KJ/kg.°C

Therefore,

`120\ KJ = (13\ kg)(0.385\ KJ/kg^oC)(T-27^oC) + (4\ kg)(4.2\ KJ/kg^oC)(T-50^oC)\\120\ KJ - 135.135\ KJ - 840\ KJ = (- 5.005T - 16.8 T)\ KJ/^oC\\T = (-855.135\ KJ)/(-28.105\ KJ/^oC)\\`

T = 30.42°C