Question

A physics class performs an experiment to determine the winner of a race. An empty can, a solid cylindrical battery and a marble roll, all with the same radius) without slipping down an inclined plane of vertical height H (they are all released at the same height). A box slides without friction on another inclined plane of the same height, H. Which object reaches the bottom of the incline first

Answer 1

a) SPHERE must be the winner

b) BOX is most fastest

Step-by-step explanation:

For this exercise we must use conservation of energy

starting point. Highest part of the plane

Em₀ = U = m g h

final point. Lowest part of the plane

Em_f = K = ½ m v² + ½ I w²

Note that as the objects roll, the kinetic energy of rotation is included. Energy is conserved

Em₀ = Em_f

mg h = ½ m v² + ½ I w²

the linear and rotational variables are related

v = w r

w = v / r

the moment of inertia of the bodies is tabulated

ring (empty can) I = m r²

cylinder I = ½ m r²

sphere (marbles) I = 2/5 m r²

mgh = ½ m v² + ½ I v²/r² = ½ mv² (+ I / mr²)

2gh / (1 + I / mr²) = v² (1)

Let's analyze the value of I / mr2

can I / mr² = mr² / mr² = 1

cylinder I / mr² = ½ mr² / mr² = ½

sphere I / mr² = 2/5 mr² / mr² = 2/5

we substitute in equation 1

v =
`\sqrt{ (2gh)/( (1+ (I)/(m r^2)) ) }`

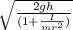
can v = √(2gh / 2) = √ gh

v = √gh

cylinder v=
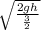`\sqrt{ (2gh)/( (3)/(2) ) }` = √(4gh/3)

v = 1,155 √gh

sphere v =
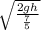`\sqrt{ (2gh)/( (7)/(5) ) }` = √(10gh/7)

v = 1.20 √gh

therefore the object with the highest speed is the one that takes less time, consequently the SPHERE must be the cattle.

b) for a box on a frictionless surface, there is no rotational kinetic energy

mgh = ½ m v²

v = √2gh

v = 1.41 √(gh)

When comparing with the latter, this would be the one that arrives first