Question

Workout to the simplest:

`\int \: {x}^(2) ln( {x}^(3) ) dx`
​

Answer 1

`\rm \displaystyle \ln(x) { {x}^(3) } - \frac{ {x}^(3) }{3} + \rm C`

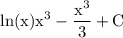
Explanation:

we would like to integrate the following integration

`\displaystyle \int {x}^(2) \ln( {x}^(3) ) dx`

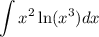
before doing so we can use logarithm exponent rule in order to get rid of the exponent of ln(x³)

`\displaystyle \int 3 {x}^(2) \ln( {x}^{} ) dx`

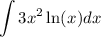
now notice that the integrand is in the mutilation of two different functions thus we can use integration by parts given by

`\rm\displaystyle \int u \cdot \: vdx = u \int vdx - \int u' \bigg( \int vdx \bigg)dx`

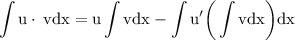
where u' can be defined by the differentiation of u

first we need to choose our u and v in that case we'll choose u which comes first in the guideline ILATE which full from is Inverse trig, Logarithm, Algebraic expression, Trigonometry, Exponent.

since Logarithms come first our

`\displaystyle u = \ln(x) \quad \text{and} \quad v = {3x}^(2)`

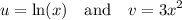
and u' is
`(1)/(x)`

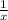
altogether substitute:

`\rm \displaystyle \ln(x) \int 3{x}^(2) dx - \int (1)/(x) \left( \int 3 {x}^(2) dx \right)dx`

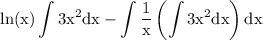
use exponent integration rule to integrate exponent:

`\rm \displaystyle \ln(x) \int 3{x}^(2) dx - \int (1)/(x) \left( 3\frac{ {x}^(3) }{3} \right)dx`

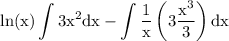
once again exponent integration rule:

`\rm \displaystyle \ln(x) 3\frac{ {x}^(3) }{3} - \int (1)/(x) \left( 3\frac{ {x}^(3) }{3} \right)dx`

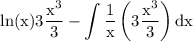
simplify integrand:

`\rm \displaystyle \ln(x) 3\frac{ {x}^(3) }{3} - \int \frac{ 3{x}^(3) }{3x} dx`

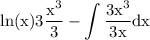
use law of exponent to simplify exponent:

`\rm \displaystyle \ln(x) \frac{ 3{x}^(3) }{3} - \int \frac{ 3\cancel{ {x}^(3)} }{3 \cancel{x}} dx`

`\rm \displaystyle \ln(x) \frac{ 3{x}^(3) }{3} - \int \frac{ 3{x}^(3) }{3} dx`

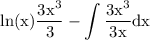
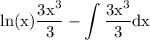
use constant integration rule to get rid of constant:

`\rm \displaystyle \ln(x) \frac{3 {x}^(3) }{3} - 1 \int {x}^(2)dx`

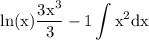
use exponent integration rule:

`\rm \displaystyle \ln(x) \frac{3 {x}^(3) }{3} - \frac{ {x}^(3) }{3}`

`\rm \displaystyle \ln(x) { {x}^(3) } - \frac{ {x}^(3) }{3}`

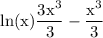
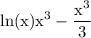
and finally we of course have to add the constant of integration:

`\rm \displaystyle \ln(x) { {x}^(3) } - \frac{ {x}^(3) }{3} + \rm C`

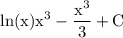
and we are done!