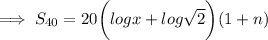Answer:
a)
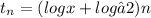
b)
![S_(40) =20\bigg(log x + log \sqrt 2\bigg)[ 1+n]](https://img.qammunity.org/2023/formulas/mathematics/high-school/82095uolnel0xlc3f11bhrz01dq5cgriks.png)
Explanation:
Given arithmetic sequence is:
log x + log √2, 2 log x + log 2, 3 log x + log 2√2......
First term a = log x + log √2
common difference d = 2 log x + log 2 - (log x + log √2)
= 2 log x + log 2 - log x - log √2
= log x + log 2 - log √2
= log x + log (√2*√2)- log √2
= log x + log √2 + log √2- log √2
= log x + log √2
(a)
General term of the arithmetic sequence is given as:
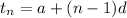
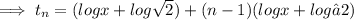
![\implies t_n = (log x + log \sqrt 2)[1+ + (n - 1)]](https://img.qammunity.org/2023/formulas/mathematics/high-school/66sce8r0nv8duq1te049fslqz3p5jvjpc0.png)
![\implies t_n = (log x + log \sqrt 2)[1+ n - 1]](https://img.qammunity.org/2023/formulas/mathematics/high-school/plc3ot9s1bbb9clnol1usmz1mtoq0f75xd.png)
![\implies t_n = (log x + log \sqrt 2)[n]](https://img.qammunity.org/2023/formulas/mathematics/high-school/97vbq5mx4q8tkcxyy2i9tuai1tklheukv3.png)
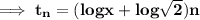
(b)
Sum of first n terms of an arithmetic sequence is given as:
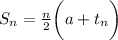
![\implies S_(40) =(40)/(2)\bigg[ (log x + log \sqrt 2)+(log x + log \sqrt 2)n\bigg]](https://img.qammunity.org/2023/formulas/mathematics/high-school/wljof0moalhu4pwwoacgahrpnnra08kgwx.png)