Given:
Coordinates of the midpoint = (2,-14)
Coordinates of one endpoint = (4,-13)
To find:
The coordinates of the another endpoint.
Solution:
Let us assume (a,b) be the another endpoint.
According to the midpoint formula:
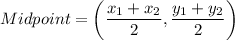
By using the midpoint formula, we get
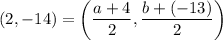
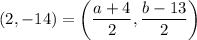
On comparing both sides, we get
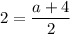
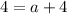
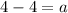
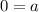
And,
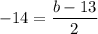
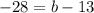
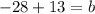
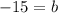
Therefore, the another end point is (0,-15).