The nearest tenth options closest one is: A
To find the measure of angle B in the triangle, you can use the Law of Cosines,
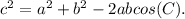
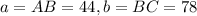 and
and
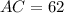
let C be the angle B.
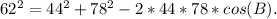
Now, solve for cos(B):
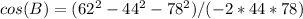
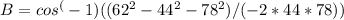
The angle B and round to the nearest tenth.
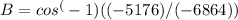
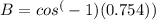
B ≈ 41.6°.
Therefore, the nearest tenth is B ≈ 41.6 °, options closest one is: (A) 37.5.