Question

Integrate( 1\x^3-3x-4)dx​

Answer 1

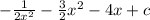`-(1)/(2x^2) - (3)/(2)x^2 -4x +c` Assuming you need the integral this would be the answer.

Explanation:

`\int\limits (1)/(x^3) -3x \, -4dx`

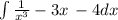
Thats after removing parenthesis.

Now we have to split into multiple intergrals..

`\int\ (1)/(x^3) \, dx + \int\ -3xdx + \int\-4dx`

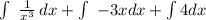
Now we want to move x^3 out of the denom by raising it to the -1 power

`\int\ (x^3)^(-1)dx + \int\- -3xdx+\int\ -4dx`

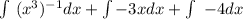
Multiply the exponents in (x^3)^-1

We also need to apply the power rule of (a^m)^n = a^mn

`\int\ x^(3*-1)dx+\int\ -3xdx + \int\ -4dx`

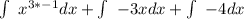
3 by -1

`\int\ x^(-3)dx+\int\ -3xdx + \int\ -4dx`

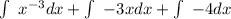
Now we want to use the power rule (I assume you know this rule so I won't be posting it) as I with the integral of x^-3 where x is -1/2x^-2

`-(1)/(2)x^(-2) + C \int\ -3xdx + \int\ - 4dx`

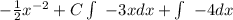
Now since -3 is a constant we can move -3 out of the integral since it respects x.

`-(1)/(2)x^(-2) + C - 3 \int\ xdx + \int\ -4dx`

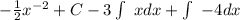
Now we need to remember the power rule with the respect to 1/2x^2 which is respective to x.

`-(1)/(2)x^(-2) + C - 3 ((1)/(2)x^2 +C)+\int -4dx`

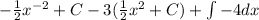
Then we apply the constat rule (You should know this as well)

`-(1)/(2)x^(-2) + C - 3 ((1)/(2)x^2+C)-4x+C`

Now we simplify....

`-(1)/(2)x^(-2) + C - 3 ((x^2)/(2)+C)-4x + C > -(1)/(2x^2) - (3x^2)/(2) -4x + C`

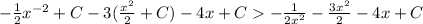
As you can see you just then re-order as above.

Answer 2

the answer is 56643

Explanation:

the best way for you to understand is to make sure you have a decent amount of credit