Question

An object accelerates 6.0 m/s2 when a force of 3.0 newtons is applied to it. What is the mass of the object?

Answer 1

`\boxed {\boxed {\sf (1)/(2) \ or \ 0.5 \ kg}}}`

Step-by-step explanation:

Force is the product of mass and acceleration.

`F=ma`

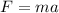
We know the force is 3.0 Newtons and the acceleration is 6.0 meters per square second.

Let's convert the Newtons to make the problem easier later.

• 1 Newton is equal to 1 kilogram meter per square second.
• The force of 3.0 N is equal to 3.0 kg*m/s²

`F= 3.0 \ kg*m/s^2 \\a= 6.0 \ m/s^2`

`3.0 \ kg *m/s^2= m (6.0 \ m/s^2)`

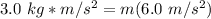
Since we are solving for mass, we must isolate the variable. It is being multiplied and the inverse is division. Divide both sides by 6.0 meters per square second.

`\frac {3.0 \ kg *m/s^2}{6.0 \ m/s^2}= (m (6.0 \ m/s^2))/(6.0 \ m/s^2)`

`\frac {3.0 \ kg *m/s^2}{6.0 \ m/s^2}=m`

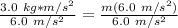
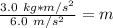
The meters per square second cancel, hence our earlier unit conversion.
`(1 )/(2) \ kg =m`

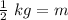
The mass of the object is 1/2 or 0.5 kilograms