Question

Please help it's just prove that...


`(1)/(2) (sin7 \alpha - sin3 \alpha ) = cos5 \alpha sin2 \alpha`
​

Answer 1

see below

Explanation:

we would like to prove the following equality:

`(1)/(2) ( \sin(7\alpha) - \sin(3 \alpha) ) = \cos(5 \alpha )\sin(2 \alpha )`

well, In order to prove the equality, we can consider utilizing the sum and product identities of trigonometry.

we can prove this equality either from LHS or RHS.recall that,

`\displaystyle\sin( x ) \cos( x ) = (1)/(2) ( \sin( x + y ) + \sin( x- y) )`

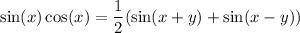
Notice that This identity can be utilised in the RSH.So,

Assign variables:

`x \implies 2 \alpha \\ y \implies5 \alpha`

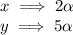
thus rewriting the RSH yields:

`\implies \displaystyle(1)/(2) ( \sin(7\alpha) - \sin(3 \alpha) ) \stackrel {?}{ = } (1)/(2) ( \sin( 2 \alpha + 5 \alpha ) + \sin( 2 \alpha - 5 \alpha ) )`

simplify:

`\implies \displaystyle(1)/(2) ( \sin(7\alpha) - \sin(3 \alpha) ) \stackrel {?}{ = } (1)/(2) ( \sin( 7 \alpha ) + \sin( - 3 \alpha ) )`

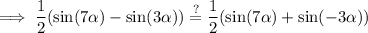
Call to mind that

• sin(-x) = -sin(x)

hence,

`\implies \displaystyle(1)/(2) ( \sin(7\alpha) - \sin(3 \alpha) ) \stackrel { \checkmark}{ = } (1)/(2) ( \sin( 7 \alpha ) - \sin( 3 \alpha ) )`

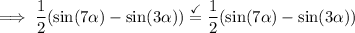
therefore,

• LSH=RSH

and we are done!