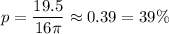Answer:
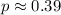
Explanation:
We are given a circle of radius 4 cm, and a triangle inscribed within the circle with a vertical height of 6.5 cm and a base of 6 cm.
To find the probability a randomly selected point lands in the red area, we can divide the red area by the total area.
The area for a circle is given by:
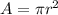
Since the radius is 4 cm, the area of the circle or total area is:
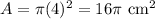
The area for a triangle is given by:

The base of the triangle is 6 cm total and the vertical height is 6.5 cm. Therefore, the area is:
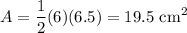
The probability of landing in the red shaded area is:

Therefore: