Question

SOMEONE HELP ME TO FIND THE VALUES OF A AND B TO MAKE THE SYSTEM OF EQUATIONS TRUE.

Answer 1

A.

`3 = a * b { }^(0)`

when it's to the 0 power it equals 1

`b {}^(0) = 1`

`3 = a * 1`

so therefore a=3

_______________

`75 = a * b {}^(2)`

replace a with 3

`75 = 3 * b {}^(2)`

divide 75 by 3 equalling 25

`b {}^(2) = 25`

lastly find the square root

`√(25) = 5`

there fore

________

b= 5

a= 3

I hope this was helpful:)

Answer 2

9514 1404 393

Answer:

a) (a, b) = (3, 5) or (3, -5)

b) (a, b) = (2, 3)

Explanation:

Generally, you solve systems like this by dividing one equation by the other. This gives you the value of the base (b). Substituting that into either equation gives you the scale factor (a).

__

a) Since b^0 = 1, you already have the solution for 'a': 3 = a. Substituting that into the second equation gives ...

75 = 3b^2

b = √(75/3) = √25 = 5

Since both exponents of b are even, there is no reason why b could not be -5.

Possible solutions: (a, b) = (3, 5) or (3, -5).

__

b) Dividing the second equation by the first gives b:

`(54)/(18)=(a\cdot b^3)/(a\cdot b^2)\\\\3=b \qquad\text{simplified}\\\\18=a\cdot3^2\qquad\text{substitute for b}\\\\(18)/(9)=a=2\qquad\text{divide by 9}`

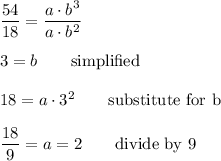
The solution is (a, b) = (2, 3).

_____

Additional comment

Usually, we're only interested in positive solutions for 'b'. Negative values usually only make sense when the exponent is an integer, as in the case of an exponential sequence.