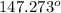Question

1. Find the sum of the measures of the interior angles of a convex 11-gon.

Answer 1

The measure of the sum of interior angles of a 11-gon is
`1620^(o)`.

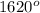Each interior angle is approximately
`147.273^(o)`.

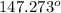Explanation:

A convex polygon has the measure of each interior angles to be less than
`180^(o)`.

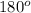But,

sum of interior angles of polygon = (n - 2) x
`180^(o)`

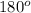
where n is the number of sides of the polygon.

For a convex 11-gon, we have;

sum of angles of a 11-gon = (11 - 2) x
`180^(o)`

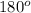
= 9 x
`180^(o)`

=
`1620^(o)`

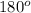
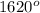
Sum of angles of a 11-gon =
`1620^(o)`

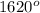
To check: convex polygons' interior angles are less than
`180^(o)`.

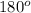so that,

each interior angle of 11-gon =
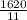
`(1620)/(11)`

=
`147.273^(o)`