Answer:
1 7142.699082ft³ (C)
2 1063.420642cm³ (A)
Explanation:
Hey There!
1. So for the first one we want to find the volume of the rectangular pool and the volume of the semi cylinder
The dimension given are
length - 45
width - 30
height - 5
to find the volume we use
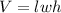

so the volume of the rectangular pool is 6750ft³
now we need to find the volume of the semi cylinder
the dimensions given are
diameter - 20
height - 2.5
so we find the volume by using the volume for a cylinder then dividing by 2
the volume for a cylinder formula is
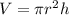
r = radius
h = height
to find the radius given the diameter we just divide by 2
20/2=10 so the radius is 10
now we just plug in the values and get

Note: the 1/2 is added because were finding the volume of a semi cylinder
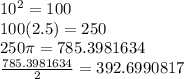
So the volume of the sitting area is 392.6990817
Now that we have found the volume of each part we add them together to get the answer
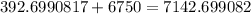
2. For the second one we need to find the volume of the cylinder and subtract it by the volume of the tennis ball..s times 4 ( because there are 4 of them)
For the cylinder we are given the dimensions
height - 39.5
diameter - 9.5
Remember this is the formula of the volume of a cylinder
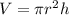
r =radius
h = height
to convert diameter to radius we divide by 2
9.5/2=4.75
now we plug in the values

so the volume of the container is 2859.100642cm³
now we need to find the volume of the tennis ball
to do this we use the formula

we are given the dimensions of
diameter - 9.5
once again to convert to radius we divide by 2
9.5/2=4.75
now we plug in the values

So the volume of the tennis bal...ls is 1795.682001
note: i multiplied by 4 because there are 4 tennis bal...ls
our final step is to subtract the volume of the bal...ls from the container
2859.100642-1795.682001=1063.420642
hope this helps :)