Question

Mr Willkinson invests £3000 at a compound interest of 2.2% per anum

he wants his investment to earn more than £800 interest
work out in the least time in years it will take​

Answer 1

if his investment were to earn an interest £800, then his accumulated amount will be 300 + 800 or namely £3800.

let's check at what point he'll be getting an accumulated amount of £3800, and then we know that compounding it further will simply result in more bucks, thus we know that'd be the least it'd take, keeping it further will simply give more.

`~~~~~~ \textit{Compound Interest Earned Amount} \\\\ A=P\left(1+(r)/(n)\right)^(nt) \quad \begin{cases} A=\textit{accumulated amount}\dotfill &\£3800\\ P=\textit{original amount deposited}\dotfill &\£3000\\ r=rate\to 2.2\%\to (2.2)/(100)\dotfill &0.022\\ n= \begin{array}{llll} \textit{times it compounds per year}\\ \textit{per annum, thus once} \end{array}\dotfill &1\\ t=years\end{cases}`

`3800=3000\left(1+(0.022)/(1)\right)^(1\cdot t)\implies \cfrac{3800}{3000}=(1.022)^t\implies \cfrac{19}{15}=1.022^t \\\\\\ \log\left( \cfrac{19}{15} \right)=\log(1.022^t)\implies \log\left( \cfrac{19}{15} \right)=t\log(1.022) \\\\\\ \cfrac{\log\left( (19)/(15) \right)}{\log(1.022)}=t\implies \stackrel{\textit{10 years, 313 days, 21hrs and 36 mins }}{10.86\approx t}`

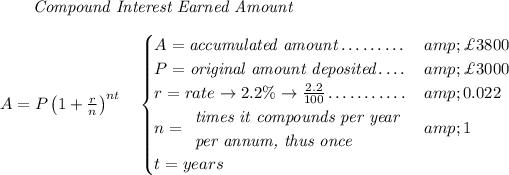
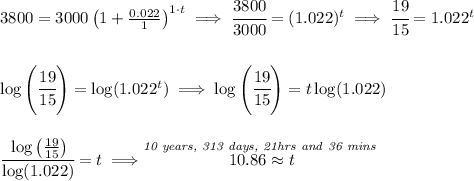
so depends, I guess if he just waits one more minute that may do it =).