a) The equations for the situation are:
Clare: 6g - 3p = 6
Noah: 8g - 9p = -42.
b) The solutions to the equations show that each goal is worth 26 points, and each penalty is worth 50 points.
Clare Noah
Goals earned 6 8
Penalties earned 3 9
Ending points 6 -42
Let the number of points earned for each goal = g
Let the number of points lost for each penalty =p
Equations:
Clare: 6g - 3p = 6
Noah: 8g - 9p = -42
Solving these equations simultaneously to find the values of g and p:
First, let's solve the first equation for g:
![[ 6g = 6 + 3p ] [ g = 1 + (1)/(2)p ]](https://img.qammunity.org/2022/formulas/mathematics/middle-school/j48wuy8j1n7crgy4hcztj1c5mkk1vwxuul.png)
Now, substitute this expression for g into the second equation:
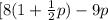
= -42 ] [ 8 + 4p - 9p
= -42 ] [ -p = -50 ]
p = 50
Now that we have the value of ( p ), we can substitute it back into the expression for g:
![[ g = 1 + (1)/(2)(50) ]](https://img.qammunity.org/2022/formulas/mathematics/middle-school/cvbqmvs46pfhu3k3ezo1rru4j8lniaym4b.png)
g = 26
Thus, each goal is worth 26 points, and each penalty is worth 50 points.