Question

Thirty middle-aged women with serum triiodothyronine (T3) readings between 180 nanograms and 200 nanograms per deciliter selected randomly from a population of similar female patients at a large local hospital. Fifteen of the 30 women were assigne d group A and received a placebo. The other 15 women were assigned to group B and received a new T3 drug. After three months, posttreatment T3 readings were taken for all 30 women and were compared with pretreatment readings. The reduction in T3 level (Pretreatment reading - Posttreatment reading) for each woman in the study is shown here.

Group A (placebo

reduction (in nanograms per deciliter): 2, 19, 8, 4, 12, 8, 17, 7, 24, 1, 3, 7, 11, 15, 9

Group B (T3 drug reduction (in nanograms per deciliter): 30, 19, 18, 17, 20, -4, 23, 10, 9, 22, 17, 21, 13, 31, 15

Part A: Do the data provide convincing evidence, at the a = 0.01 level, that the T3 drug is effective in producing a reduction in mean T3 level? (6

points) Part B: Create and interpret a 99% confidence interval for the difference in the placebo and the new drug (4 points)

Answer 1

Part A

The data provides convincing evidence that the T3 drug is effective in producing a reduction in mean T3 level

Part B

The 99% confidence interval for the difference in the placebo and the new drug is (-15.92, 0.7195)

Step-by-step explanation:

Part A

The table of data values for the study is presented here as follows;

`\begin{array}{ccc}Group \, A \ (Placebo)& Group \, B \ T3 \ drug \ reduction \ (ng/dL)\\2&30\\19&19\\8&18\\4&17\\12&20\\ 8&-4\\17&23\\7&10\\24&9\\1&22\\3&17\\7&21\\11&13\\15&31\\9&15\\\end{array}`

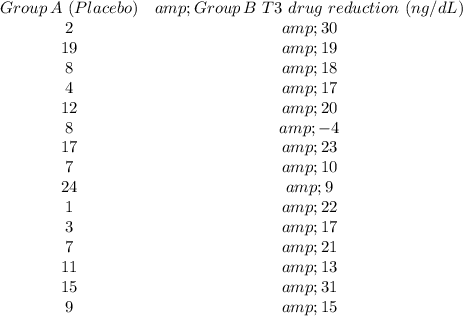
The mean for Group A,
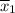`\overline x_1` = 9.8

The standard deviation for Group A, s₁ ≈ 6.614

The number of members of Group A, n₁ = 15

The mean for Group B,
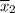`\overline x_2` = 17.4

The standard deviation for Group B, s₂ ≈ 8.56738

The number of members of Group A, n₂ = 15

The confidence level, α = 0.01 level

The null hypothesis, H₀:
`\overline x_1` ≤
`\overline x_2`

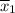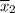
The alternative hypothesis, Hₐ:
`\overline x_1` >
`\overline x_2`

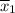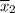
The t-test formula as follows;

`t=\frac{\overline x_(1)-\overline x_(2)}{\sqrt{(s_(1)^(2) )/(n_(1))-(s _(2)^(2))/(n_(2))}}`

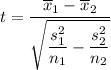
Plugging in the values of the variables, we get;

`t=\frac{ 17.4 - 9.8}{\sqrt{(8.56738^(2))/(15) - (6.614^(2) )/(15)}} \approx 5.405`

The critical 't' value at 0.01 convincing level and df = 15 - 1 = 14 is 2.624

Therefore, given that the t value is larger than the critical 't', we reject the null hypothesis and we fail to reject the alternative hypothesis, and there is convincing evidence that at a confidence level of a = 0.01, the T3 drug is effective in producing a reduction in mean T3 level

Part B

The 99% confidence interval is given by the following formula;

`\left (\bar{x}_(1)- \bar{x}_(2) \right )\pm t_(\alpha /2)\sqrt{(s_(1)^(2))/(n_(1))+(s_(2)^(2))/(n_(2))}`

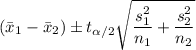
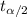`t_(\alpha /2)` = 2.977

Plugging in the values, we get;

`C.I. = \left (9.8- 17.4\right )\pm 2.977 * \sqrt{(6.614^(2))/(15)+(8.56738 ^(2))/(15)}`

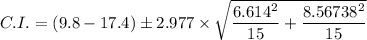
The 99% confidence interval for the difference in the placebo and the new drug is C.I. = -15.92 <
`\overline x_1` -
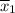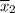`\overline x_2` < 0.7195