Question

The sum of two consecutive integers is three times their difference. what is the larger number?​

Answer 1

`\huge\boxed{2}`

Explanation:

In order to find the two consecutive numbers, we have to note that a consecutive number is one that is just after the previous.

Such: 4, 5, 6 are consecutive. 12, 69, 42 are not.

Therefore - we can represent our first number as
`x` and our second as
`(x+1)`.

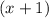Let's make an equation based on the problem.

"The sum of two consecutive integers"

• 
  `x + (x+1)`

"3 times their difference"

• 
  `3(x - (x+1))`

We can now set these equal to each other.

• 
  `x + (x+1) = 3(x - (x+1))`

Let's solve for x.

• 
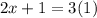  `2x + 1 = 3(1)` (Combine like terms)
• 
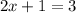  `2x+1=3` (Multiply the right side)
• 
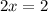  `2x = 2` (Subtract 1 from both sides)
• 
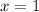  `x=1` (Divide both sides by 2)

Now we know that our first number is 1. Therefore, since our second number is one greater, our second number will be
`1+1=2`.

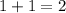The question asks for the larger number. 2 is larger than 1, therefore 2 is our answer.

Hope this helped!