So, based on the angle values that have been found, the angle of elevation of the nozzle can be 16° or 74°.
Introduction
Hi ! This question can be solved using the principle of parabolic motion. Remember ! When the object is moving parabolic, the object has two points, namely the highest point (where the resultant velocity is 0 m/s in a very short time) and the farthest point (has the resultant velocity equal to the initial velocity). At the farthest distance, the object will move with the following equation :
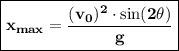
With the following condition :
 = the farthest distance of the parabolic movement (m)
= the farthest distance of the parabolic movement (m)
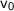 = initial speed (m/s)
= initial speed (m/s)
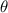 = elevation angle (°)
= elevation angle (°)- g = acceleration due to gravity (m/s²)
Problem Solving :
We know that :
 = the farthest distance of the parabolic movement = 2.5 m
= the farthest distance of the parabolic movement = 2.5 m
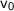 = initial speed = 6.8 m/s
= initial speed = 6.8 m/s- g = acceleration due to gravity = 9.8 m/s²
What was asked :
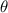 = elevation angle = ... °
= elevation angle = ... °
Step by Step :
- Find the equation value
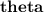 (elevation angle)
(elevation angle)

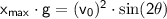
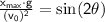


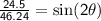
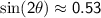
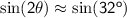
- Find the angle value of the equation by using trigonometric equations. Provided that the parabolic motion has an angle of elevation 0° ≤ x ≤ 90°.
First Probability
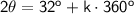

→
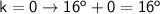 (T)
(T)
→
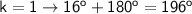 (F)
(F)
Second Probability
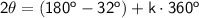
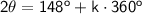
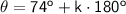
→
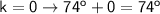 (T)
(T)
→
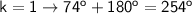 (F)
(F)
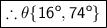
Conclusion
So, based on the angle values that have been found, the angle of elevation of the nozzle can be 16° or 74°.