Question

La ecuación de la recta que pasa por los puntos (2,-1) y (1,-5) es:

y= 4x+9




y= 4x-9




y= x-9


ninguna de las anteriores

Answer 1

Given:

A line passes through the points (2,-1) and (1,-5).

To find:

The equation of the line.

Solution:

If a line passes through the two points, then the equation of the line is

`y-y_1=(y_2-y_1)/(x_2-x_1)(x-x_1)`

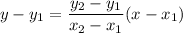
The line passes through the points (2,-1) and (1,-5). So, the equation of the line is

`y-(-1)=(-5-(-1))/(1-2)(x-2)`

`y+1=(-5+1)/(-1)(x-2)`

`y+1=(-4)/(-1)(x-2)`

`y+1=4(x-2)`

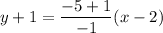
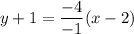
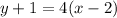
Using distributive property, we get

`y+1=4(x)+4(-2)`

`y+1=4x-8`

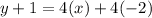
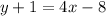
Subtract 1 from both sides.

`y+1-1=4x-8-1`

`y=4x-9`

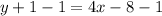
Therefore, the correct option is B.