Question

. Do the points P (-2, -3), Q (4, 1) and R (2, 4) form a right triangle?

Answer 1

Since the length of the sides respects the Pythagorean theorem, these points form a right triangle.

Explanation:

Distance between two points:

Suppose that we have two points,
`(x_1,y_1)` and
`(x_2,y_2)`. The distance between them is given by:

`D = √((x_2-x_1)^2+(y_2-y_1)^2)`

Right triangle:

Sum of the squares of the two smaller sides is equal to the square of the largest side(Pythagorean theorem).

Length of side PQ:

P (-2, -3), Q (4, 1)

`a = √((4 - (-2))^2+(1 - (-3))^2) = √(6^2 + 4^2) = √(52)`

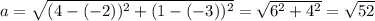
Length of side PR:

P (-2, -3), R (2,4)

`b = √((2 - (-2))^2+(4 - (-3))^2) = √(4^2 + 7^2) = √(65)`

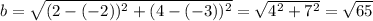
Length of side QR

Q (4, 1), R (2,4)

`c = √((2 - 4)^2+(4 - 1)^2) = √(2^2 + 3^2) = √(13)`

Pythagorean Theorem:

Smaller sides: a and c

Largest side: b

So

`a^2 + c^2 = b^2`

`(√(52))^2 + (√(13))^2 = (√(65))^2`

`52 + 13 = 65`

`65 = 65`

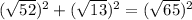
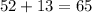
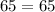
Since the length of the sides respects the Pythagorean theorem, these points form a right triangle.