Question

Can someone help me with this please?

Answer 1

1) m∠AB'C = 41°

2) m∠BAC = 49°

3) m∠B'AC = 49°

4) m∠ACB = 90° Given

5) m∠ACB' = 90°

6)
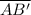`\overline {AB'}` = 24

7) Isosceles triangle

8) True

Explanation:

Given that triangle ΔABC, is the reflection of ΔAB'C, and given that a reflection is a rigid transformation, we have;

1) ΔABC ≅ ΔAB'C Given

∴ m∠AB'C ≅ m∠ABC given that Corresponding Parts of Congruent Triangles are Congruent (CPCTC)

m∠AB'C = m∠ABC by the definition of congruency

∴ m∠AB'C = m∠ABC = 41°

2) Similarly, we have;

m∠BAC = 180° - (90° + 41°) = 49° Given the sum of interior angles of a triangle theorem

m∠BAC = 49°

3) m∠BAC = m∠B'AC by CPCTC

∴ m∠B'AC = m∠BAC = 49° by transitive property

m∠B'AC = 49°

4) m∠ACB = 90° Given

5) ∴ m∠ACB' = 90° given that the sum of angles on a straight line is 180°

6)
`\overline {AB}` = 24 Given

`\overline {AB}` ≅
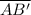`\overline {AB'}` given that ΔABC ≅ ΔAB'C and CPCTC

`\overline {AB}` =
`\overline {AB'}`

`\overline {AB'}` =
`\overline {AB}` = 24

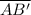
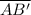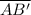`\overline {AB'}` = 24

7) In ΔABB',
`\overline {AB'}` =
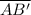`\overline {AB}` = 24 therefore, ΔABB' has two sides equal and ΔABB' Is an isosceles triangle

8) True, the angles opposite the congruent sides are the base angles of the isosceles triangle and they are therefore congruent