Question

Use the fundamental identities to fully simplify the expression.

tanx sinx+ secx cos^2x. Explain how you do it

Answer 1

First, remember that:

`tan(x) = (sin(x))/(cos(x))`

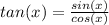
and:

`sec(x) = (1)/(cos(x))`

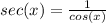
Then we can rewrite the expression:

`tan(x)*sin(x) + sec(x)*cos^2(x) = A`

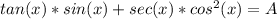
Where A is an equivalent expression.

as:

`(sin(x))/(cos(x)) *sin(x) + (1)/(cos(x))*cos^2(x) = A`

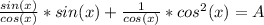
Then this is:

`(sin^2(x))/(cos(x)) + cos(x) = A`

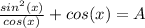
Now we can multiply both sides by cos(x), then:

`((sin^2(x))/(cos(x)) + cos(x))*cos(x) = A*cos(x)`

`sin^2(x) + cos^2(x) = A*cos(x)`

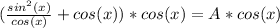
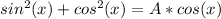
And we know that the left term of the above equation is equal to 1, then:

`1 = A*cos(x)`

`(1)/(cos(x)) = sec(x) = A`

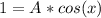
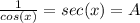
And A is equivalent to the original expression, then we get:

`tan(x)*sin(x) + sec(x)*cos^2(x) = sec(x)`

The simplification of the expression is sec(x)