Question

What is the volume of the following shape?

Answer 1

`V=V_(1)+V_(2)=96+36=132\: cm^(3)`

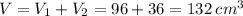
Explanation:

We can divide it into two parts:

First, we can fin the volume of the parallelepiped:

h1 = 16 cm

w1 = 2 cm

d1 = 3 cm

`V_(1)=h_(1)*w_(1)*d_(1)=16*2*3=96\: cm^(3)`

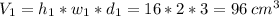
Now, the volume of the second parallelepiped is:

h2 = (8-2) cm = 6 cm

w2 = 2 cm

d2 = 3 cm

`V_(2)=h_(2)*w_(2)*d_(2)=6*2*3=36\: cm^(3)`

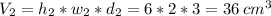
Finally, the total volume will be the addition of these two volumes.

`V=V_(1)+V_(2)=96+36=132\: cm^(3)`

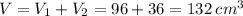
I hope it helps you!