Angles A and B are vertical angles. The measure of angle A is 8x + 1 and angle B is 21 – 2x. Find each angle measure.

Question

asked Jul 18, 2022 146k views

1 Answer

ShivaPrasad · Answer 1 · 2022-07-24T19:04:00+0000

Given:

Angles A and B are vertical angles.

The measure of angle A is 8x + 1 and angle B is 21 – 2x.

To find:

The measure of each angle.

Solution:

We know that vertically opposite angles are always equal.

Angles A and B are vertical angles.

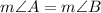
$m\angle A=m\angle B$

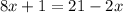
8x+1=21-2x

Isolate variable terms.

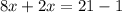
8x+2x=21-1

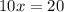
10x=20

Divide both sides by 10.

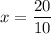
x=(20)/(10)

x=2

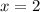
Now,

$m\angle A=8x+1$

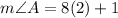
$m\angle A=8(2)+1$

$m\angle A=16+1$

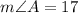
$m\angle A=17$

And,

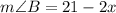
$m\angle B=21-2x$

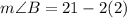
$m\angle B=21-2(2)$

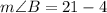
$m\angle B=21-4$

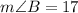
$m\angle B=17$

Therefore, the measure of angle A and angle B is 17 degrees.