Question

part A- calculate the measure if Part b- calculate the measure of

PLEASE HELP ME ITS DUE In 10 mins please

Answer 1

Explanation:

Part A

Since, BDFHJ is a regular pentagon,

Measure of interior angles of this pentagon =
`((n-2)* 180)/(n)`

=
`((5-2)* 180)/(5)`

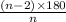
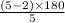
= 108°

Since, ∠ABC ≅ ∠JBD [Vertical angles]

Therefore, m∠ABC = m∠JBD = 108°

Part B

m∠JBD + mCBD = 180° [Linear pair of angles]

108° + m∠CBD = 180°

m∠CBD = 180 - 108

m∠CBD = 72°

Similarly, m∠BDF + m∠CDB = 180°

m∠CDB + 108° = 180°

m∠CDB = 180 - 108

= 72°

In ΔCBD,

m∠BCD + m∠CDB + m∠DBC = 180°

m∠BCD + 72° + 72° = 180°

m∠BCD = 180° - 144°

= 36°