Question

The two trains above are docked at St. Mark's Train Station and are assigned to parallel tracks.

At 7am, Train #941 leaves the station traveling 48 mph. Three hours later, Train #940 leaves
the station traveling in the same direction as Train #941. At 5pm, Train #940 catches Train
#941.
Find the speed of Train #940.
Helppppp

Answer 1

The speed of Train #940 is 68.
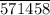`\overline{571458}` mph

Explanation:

The given parameters of the w=question are;

The time at which train #941 leaves the station = 7 a.m.

The speed with which train #941 travels, v = 48 mph

The time at which train #940 leaves the station = 3 hours after train #941

Therefore;

The time at which train #940 leaves the station = 3 hours + 7 a.m. = 10 a. m.

The direction of train #940 = The direction of train #941

The time at which train #940 catches train #941 = 5 p.m.

We have;

The time, 't', (after departure of train #941) it takes train #940 to catch train #941, is given as follows;

t = 5 p.m. - 7 a.m.

∴ t = 17:00 hours - 07:00 hours = 10 hours

The time (after departure of train #941) it takes train #940 to catch train #941, t = 10 hours

The distance from St. Mark's Train Station train #940 catches Train #941, 'd', is given as follows;

d = The speed of travel of train #941 × t

∴ d = 48 mph × 10 h = 480 miles

The distance from St. Mark's Train Station train #940 catches Train #941, d = 480 miles

The time train

The time, t₂, it takes Train #940 to catch up with train #941 is given as follows;

t₂ = 5 p.m. - 10 a.m. = 17:00 hours - 10:00 hours = 7 hours

The speed of Train #940, v₂ = d/t₂

∴ v₂ = (480 miles)/(7 hours) = 68.
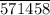`\overline{571458}` mph

The speed of Train #940, v₂ = 68.
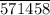`\overline{571458}` mph